Conceptos previos 

Para poder acometer este tipo de construcciones los antiguos egipcios deberían tener un mínimo de conocimientos tanto geométricos como aritméticos, así como una buena técnica de dibujo.

La siguiente figura da una idea de cómo pudo ir evolucionando la geometría y el dibujo.

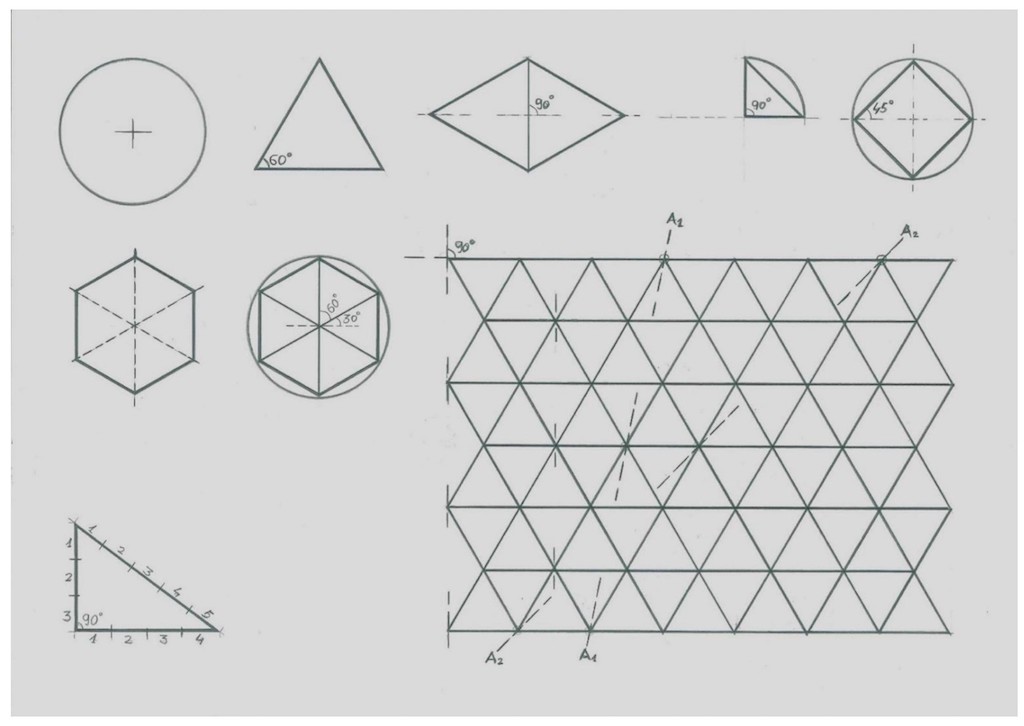 Dibujo 5

En el dibujo están representadas las figuras geométricas más normales y su evolución y composición. La más elemental podría ser el círculo por ser la más intuitiva (aparece mucho en formas naturales), un compás primario son dos ramitas que forman una horquilla; la siguiente sería un triángulo equilátero, se hace con tres segmentos iguales. A partir de estas dos podemos empezar a desarrollar un conjunto de figuras geométricas, ángulos y figuras compuestas hasta el infinito. Los antiguos egipcios, es de suponer, disponían de conocimientos geométricos; al menos prácticos. 

El dibujo muestra una mínima evolución de figuras, trazado de ángulos, representación de mallas de gran utilidad a la hora de replantear superficies y ángulos, incluso debían poseer una cierta técnica para dibujar y construir figuras tridimensionales.

También desde muy antiguo conocían el triángulo “mágico” de lados con longitudes 3 4 y 5 (el triángulo pitagórico), que permite trazar rectas perpendiculares. Es posible que, al menos de forma práctica, intuyeran el Teorema de Pitágoras, simplemente representar mallas de cuadrados de 3 x 3 4 x 4 y 5 x 5 y contando el número de cuadrados. 

Lo cierto es que de no haber poseído un conocimiento geométrico muy desarrollado, al menos de forma práctica, los antiguos egipcios habrían sido incapaces de realizar las pirámides tan colosales y tan bien ejecutadas que nos han legado.

Esto es un ejemplo elemental de la evolución primigenia, pero durante cientos de años la evolución tuvo que ser mucho más compleja de lo representado, y no solo técnicamente, su planificación tuvo que ser excepcional pues utilizaron, además de las canteras cercanas a la pirámide otras situadas a cientos de kilómetros. Es como si el PERT (Técnica de Revisión y Evaluación de Proyectos) lo inventaran ellos y no en 1957 en el proyecto Polaris de los EE. UU.

Primeros trabajos  

Ya hemos indicado que lo primero que hay que hacer es elegir el sitio para construir la pirámide y lo siguiente hacer la cimentación. Hay que nivelar un cuadrado de 230 m de lado.

En la base de la pirámide se ha detectado un “error” de 2 cm ¡Increíble! Debemos definir cómo podemos conseguir esta precisión. Hay algún estudio que dice que hay que hacer una especie de estanque alrededor de la pirámide y rellenarlo de agua. La idea es buena, pero… si, por ejemplo, le damos una profundidad de 50 cm deberemos aportar 26.450 m3 de agua y el rio está lejos y a un buen desnivel, con el inconveniente de que la caliza tiene muchas grietas y habría muchas filtraciones; por no hablar de la evaporación que se produciría. Hay otro inconveniente, ya hemos apuntado que de las 203 hiladas que quedan hay 83 con un error de nivelación igual o inferior a 2 cm ¿Cómo lo conseguiríamos?

El sistema diseñado se compone de un canal de madera de sección triangular de algo más de 6 m de longitud, que puede adosarse a otros y rellenaremos de agua. El consumo de agua sería mínimo y la precisión total, el nivel de agua no miente. Al adosarlos podríamos tener cualquier longitud, aunque sería aconsejable no pasar de 30 m.

El canal está representado en la figura, tiene unas acanaladuras horizontales para comprobar el nivel de agua. Una de las ventajas que tiene es que consume poca agua, además se pueden utilizar en todas las hiladas que componen la pirámide. Sería algo semejante a un “nivel de burbuja” para grandes superficies.

El canal tendría unas pequeñas plomadas laterales para hacer más fácil la nivelación.

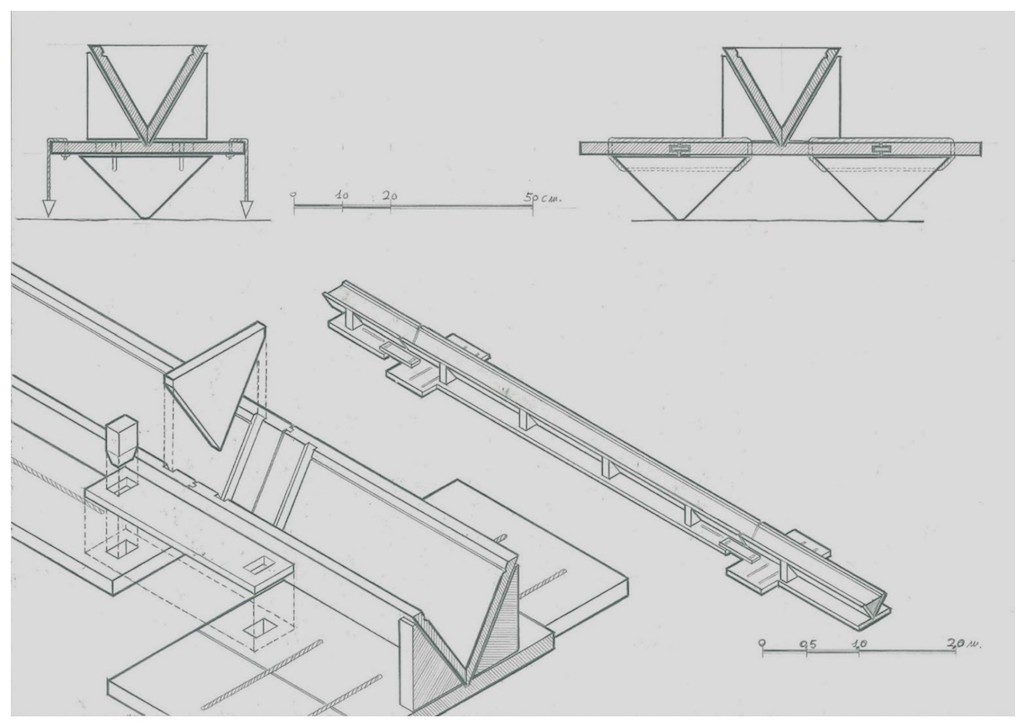Dibujo 6 

Una vez realizado el replanteo aproximado de la planta donde se cimentará la pirámide, se procederá a su nivelación. Para nivelar utilizaremos el agua. En la figura vemos el método: construiríamos unos canales de madera que llenaremos de agua, como el que ve en la figura, de unos 6,5 m de longitud que apoyará en tres puntos; uno en un extremo y los otros dos en el contrario. La sección es triangular, con lo que el consumo de agua es pequeño. Se puede alargar mediante cuñas de unión, y su longitud puede ser tan larga como queramos. En su parte superior llevará unas acanaladuras que servirán para comprobar la horizontalidad de la superficie que estemos nivelando.

Podemos considerar que es una especie de “nivel de burbuja”, pero para grandes distancias. También lo podremos utilizar para nivelar las sucesivas hiladas que vayamos añadiendo a la pirámide. Si además lo instrumentamos con pequeñas plomadas, dejando un punto fijo y girando a su alrededor podremos conseguir nivelaciones con un error menor de un milímetro.

Todas las juntas e uniones se impermeabilizarán con esparto o cualquier otro material impermeable, como la arcilla, cera, brea … En las perspectivas inferior izquierda y central se describe la forma de unir entre sí varios canales.

Este canal se complementaría con otro triangular de unos 5 m. de lado e idéntica sección. El primero se utilizará preferentemente para nivelaciones lineales y el segundo para superficiales.

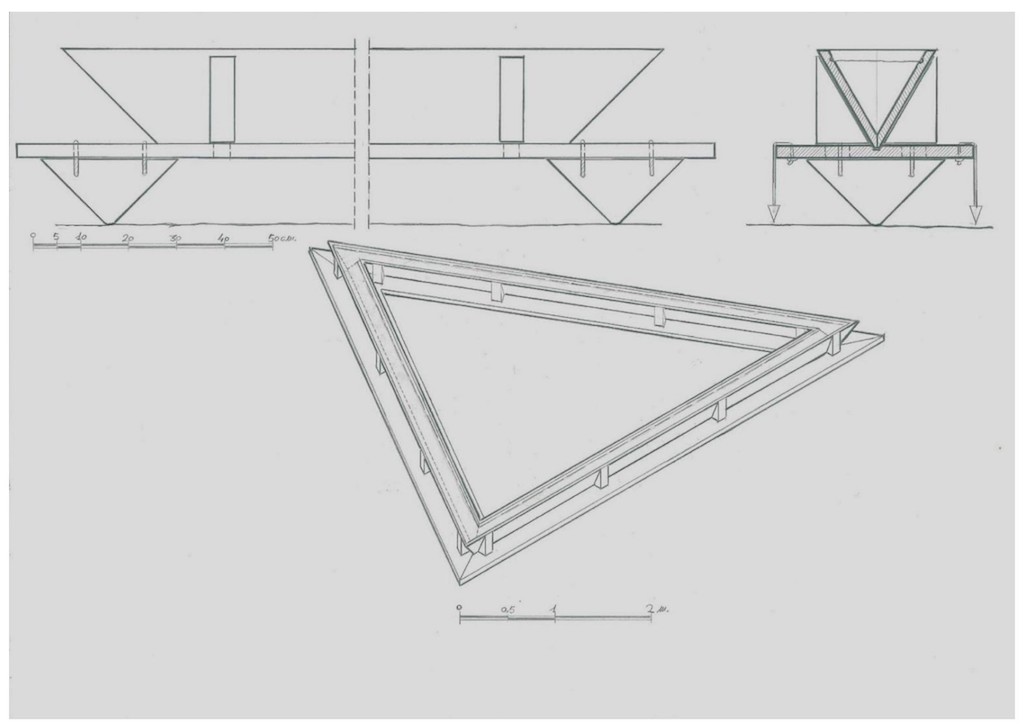Dibujo 7

Este sería otro tipo de nivel de agua que complementaría al anterior. Se trata de un triángulo equilátero de unos 5 m de lado que nos permite trabajar sobre grandes superficies. Su diseño es similar al del “canal nivelador”, una sección en cuña con acanaladuras superiores y dotado de varias plomadas, que al ir girando y desplazándose se pueden conseguir unos errores de nivelación prácticamente despreciables. Se podrá utilizar a cualquier altura durante la construcción de la pirámide y su manejo, montaje, mantenimiento y reparación es rápido y sencillo.

Uno de los dilemas al que aún no hemos hecho referencia es la orientación de la Gran pirámide. Está perfectamente orientada a los cuatro puntos cardinales con un error máximo de 5 minutos de grado, lo cual es prácticamente despreciable. Hay varias teorías de cómo pudieron ser tan precisos y en general son correctas: bien por la posición que tomaba el sol por el día, bien por las estrellas durante la noche. Como en este estudio intentamos resolver el mayor número de interrogantes, proponemos una nueva solución: Una de las peculiaridades climatológicas de Guiza es que el número de horas de sol es muy elevado; prácticamente no llueve. Así pues, utilizaremos la trayectoria del sol para determinar la orientación de los ejes. Los antiguos egipcios consiguieron orientarlos con error del 1 por 1.000. Veamos como lo haríamos.

Lo primero sería explanar un cuadrado de 30 x 30 m en el centro de la cara norte con una precisión de nivelación de 2 mm, lo cual es factible con los canales niveladores. Después, en el centro y al sur del cuadrado anclaríamos un poste de unos 12 m acabado en punta y con una ligera inclinación hacia el norte. Con ayuda de la plomada proyectaríamos la punta en el suelo, y tomándola como centro dibujaríamos dos círculos: uno de 10 m de radio, y el otro de 12 m, ambos con un grosor de línea de 1 mm. Cada cinco días, observaríamos y marcaríamos en el suelo la sombra de la punta del poste, desde que amanece hasta que se pone el sol, obteniendo de esta manera los cuatro puntos de intersección con los otros dos círculos. Uniendo los dos puntos da cada círculo iríamos marcando orientaciones este – oeste, que compararíamos entre si hasta obtener un valor medio. Pienso que el sistema nos daría suficiente precisión.

Una vez determinado el eje oeste debemos replantear la planta de la pirámide, algo complicado. Se ha detectado en algunas partes de su interior que existen puntos del terreno natural de altura superior a la base. Es como si hubieran tallado plataformas aprovechando la topografía del terreno. Este dato complica su replanteo pues no se ven entre sí los cuatro puntos del cuadrado, es decir, no podemos utilizar las dimensiones de sus diagonales para completar el replanteo. La forma de ajustar su base se representa en la siguiente figura.

Dibujo 8

 Esta figura representa la planta de la pirámide y su replanteo. Como hay indicios de la existencia de plataformas internas escalonadas labradas en la propia roca, se representan las correspondientes a las siete primeras hiladas y que coinciden con los bloques de más altura.

Para replantear este tipo de obras donde no se divisa el vértice opuesto, utilizaremos la triangulación. Comenzaremos por el punto ”A”, donde situaremos uno de los vértices de la pirámide, y a partir de éste se fijará el eje este-oeste sobre el que marcaremos otro punto a una distancia de 15 m. A partir de estos dos puntos se irán distribuyendo triángulos equiláteros alrededor de la primera de las terrazas escalonadas y por todo el perímetro de la base

Poco a poco iremos cerrando el cuadrado que delimita la pirámide y comprobando que tanto las alineaciones de los vértices de los triángulos como las que unen vértices no consecutivos ( L2 L3 L4) no presentan desviaciones significativas. Siempre tendríamos algún error acumulado por estiramiento de las cuerdas, alineaciónes de puntos etc. Error que teniendo en cuenta que son necesarias 33 medidas para completar la diagonal estaría comprendido entre 33 y 66 cm.

El error de cierre que se producirá en el punto “B”, es el que tendremos que evaluar para considerar que la base está correctamente replanteada. Teniendo en cuenta que el error máximo detectado entre las longitudes de los lados del cuadrado de la base es de 20 cm, podríamos admitir en el punto “B” un desfase máximo de 50 cm, equivalente al codo egipcio (52,4 cm). Las nuevas alineaciones irían desde las rectas R1 y R2 hasta el centro de la distancia que se ha desviado el punto “B”. Una vez corregidas las alineaciones, no sería muy complicado determinar las longitudes de los cuatro lados (algo más de 230 metros).

En la siguiente perspectiva se representa idealizada la posible utilización del terreno natural como base de cimentación. Esta solución sería beneficiosa para la estabilidad de la pirámide, además del ahorro que supone la fabricación y colocación de los bloques más grandes que componen su núcleo.

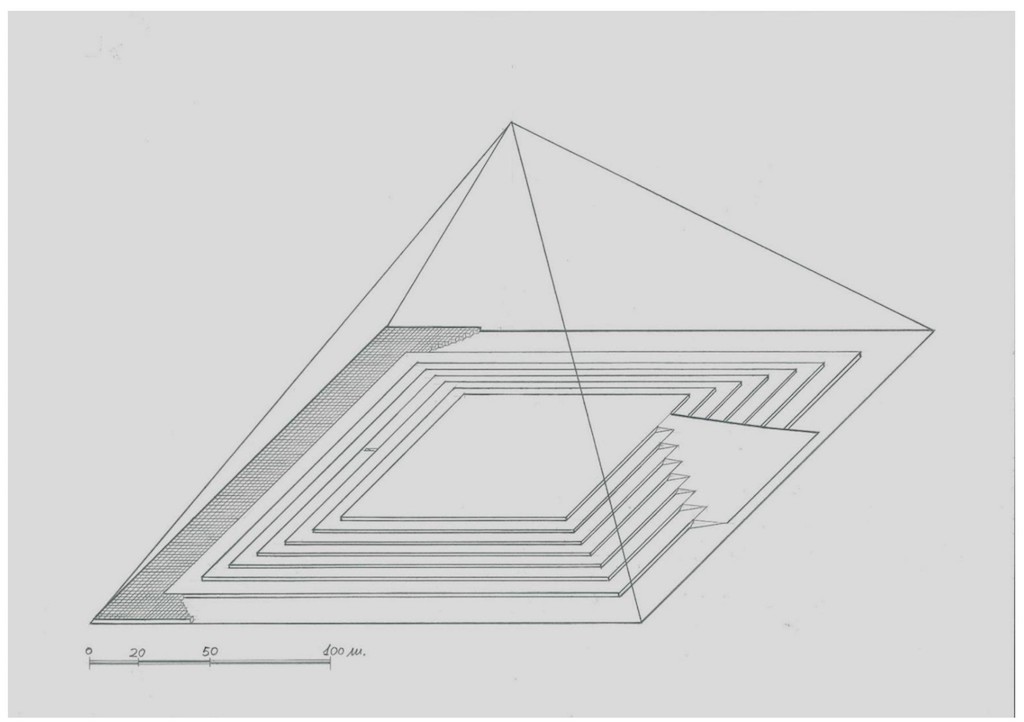Dibujo 9

Una hipótesis que no debemos olvidar es la posibilidad de utilizar la colina donde se sitúa la pirámide como cantera. Se supone que se eligió el sitio porque el terreno rocoso era homogéneo. Esto facilitaría enormemente el inicio de los trabajos pues al tiempo que vamos tallando la pequeña “pirámide escalonada” que conforma el núcleo, iríamos fabricando los bloques más pesados que componen las primeras hiladas. En este dibujo están representadas idealmente las siete terrazas que componen el núcleo de la pirámide, que es donde colocaríamos las siete primeras hiladas.

Desconozco la verdadera altura de las terrazas, cuantas eran y que forma tenían. En esta recreación las he adaptado a la altura de las siete primeras hiladas de la Gran Pirámide y se han representado cuadradas. Realmente su forma y su número dependerá de la orografía inicial del terreno.

En la parte derecha situaríamos las rampas, pueden ser “tradicionales” (arena grava y adobes) y las utilizaríamos en caso de poder extraer bloques de la propia colina. Supondría una cantera más, fabricaríamos los bloques más voluminosos y su colocación sería relativamente cómoda. Es más fácil bajarlos que subirlos.

En una de las terrazas y a la izquierda se aprecia el inicio de la posible excavación del Corredor Descendente. A pesar de la escala se empieza a reconocer la gran cantidad de bloques necesarios para completar la primera de las hiladas.

Rampas de peldaños

Si para subir los bloques no podemos utilizar rampas de arena grava y limo por sus características estructurales, la opción lógica es utilizar la propia pendiente de la pirámide, pero la pendiente en la pirámide de Keops es de 51º 50, y lo peor, el revestimiento es de caliza blanca de Tura, y no podemos dañarla.

Una buena opción es utilizar madera para su protección pues su dureza es muy inferior a la de la piedra caliza y permite que los trineos deslicen fácilmente por ella. En este estudio se propone para la subida de trineos una rampa de “peldaños”. Consiste en cortar un tablón cuadrado de 15 x 15 cm por su diagonal y apoyar ésta sobre la superficie caliza de la cara de la pirámide. Se ha elegido una rampa de 1,8 m de ancho, aunque se puede elegir cualquier otra dimensión.

Esta rampa permite utilizar muchas simultáneamente, así como acceder a distintas alturas, y lo más importante podemos llegar a la cima de la pirámide a algo más de 146 m. Otra función, y muy útil, es utilizarla como escalera para la subida y bajada de trabajadores eso sí, utilizando cuerdas como pasamanos.

Como se ve en la perspectiva es necesario anclar la rampa tanto a la superficie plana de la hilada como también a la piedra que forma la primera rampa de 15º en su inicio. De no ser así se podría desestabilizar la rampa al posicionarse sobre ella los trineos cargados.

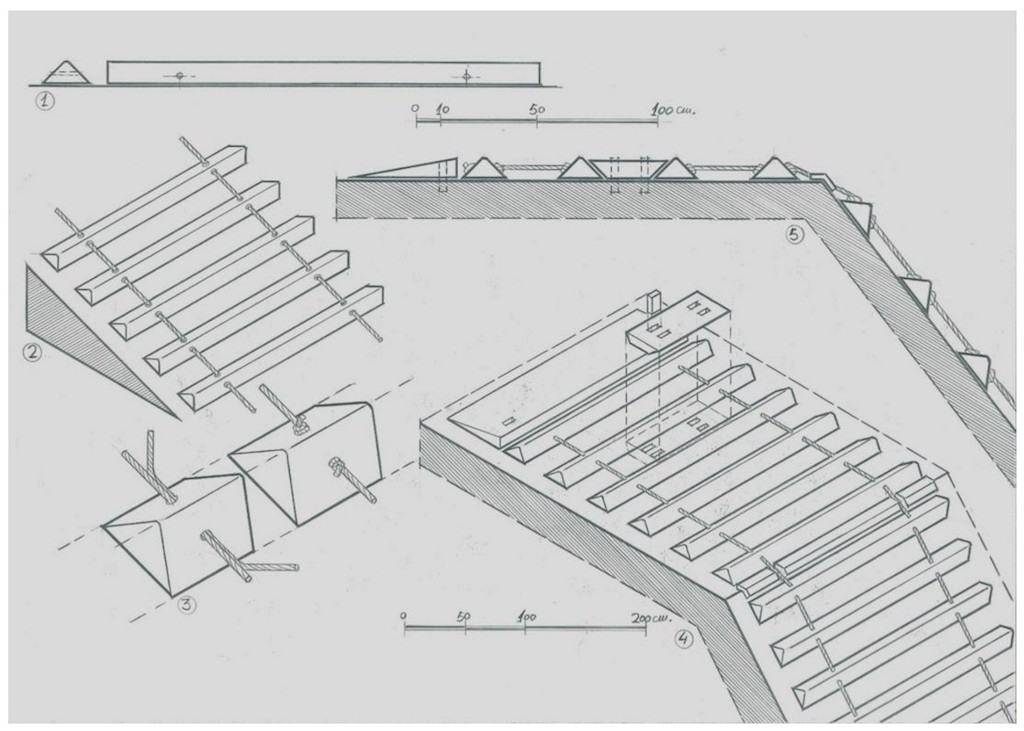Dibujo 10

Para el diseño de las rampas que utilizaremos para subir los bloques en altura elegiremos como materiales madera y cuerdas, y las denominaremos “rampas de peldaños”.

En el punto “1” vemos el módulo elemental que se utilizará: un tablón cortado por su diagonal con dos taladros paralelos a la base de apoyo, de 1,80 m de largo y sección en forma de triángulo rectángulo isósceles de lados 15 cm, con apoyo sobre su hipotenusa de 21 cm, la separación a ejes entre dos “peldaños” es de 40 cm.

En el punto “2” se aprecia cómo se va confeccionando la rampa: iríamos uniendo peldaños entre sí utilizando cuerdas -una especie de enhebrado-. Pueden adaptarse a cualquier pendiente y con cualquier separación entre peldaños.

En el punto “3” aparece el detalle de fijación de los peldaños de la rampa. Para ello se introduce una cuerda corta que se anuda a la principal impidiendo su desplazamiento.

En los apartados “4” y “5” vemos la perspectiva y la sección de la disposición de la rampa. Para evitar deslizamientos se fijará la parte horizontal mediante cuñas trapezoidales de madera al suelo. En el vértice del ángulo de la pirámide se colocarán unos angulares de madera que, por un lado, impiden el desgaste de las cuerdas de arrastre, y por otro permiten una transición menos agresiva del trineo con su carga desde la rampa inclinada a la horizontal. Por último y como remate al tramo horizontal se adosará una cuña de madera para el desembarco del trineo sobre la superficie de la pirámide.

En la sección podemos apreciar que las traviesas de madera pueden utilizarse como los peldaños de una escalera permitiendo a los trabajadores la subida y bajada a cualquier altura de la pirámide.

El peso de cada uno de los “peldaños” será de 14 kg y su volumen de 20 decímetros cúbicos.

Considerando que el máximo número de rampas que podemos montar simultáneamente estaría a la mitad de su altura, unos 75 metros, y una longitud sobre su inclinación de 96 metros. Podemos estimar que el volumen total de madera estaría alrededor de los 178 metros cúbicos. Nada escandaloso si lo comparamos con las dimensiones de la pirámide.

Este tipo de rampas permite trabajar simultáneamente a varias alturas. Lo podemos ver en la siguiente perspectiva.

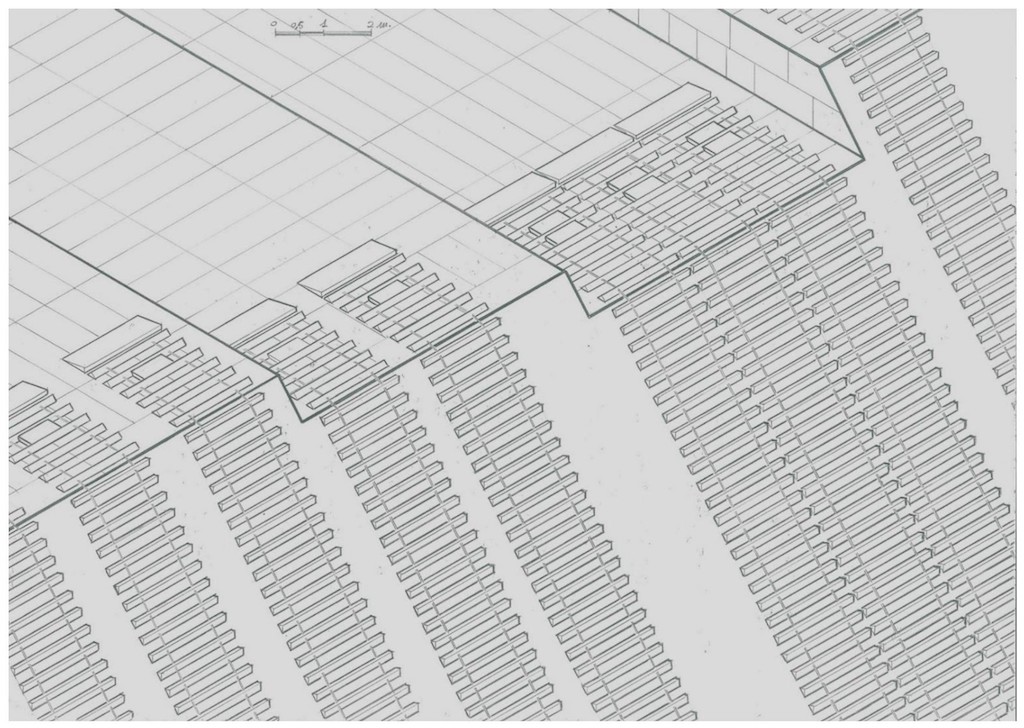Dibujo 11

La rampa proyectada es modulable y adaptable. En el dibujo se ven distintas posibilidades: puede haber rampas a distintas alturas, diversas separaciones o incluso se pueden unir varias creando una rampa más ancha. La distancia entre los peldaños también puede variar, en este diseño es de 40 cm a ejes de peldaños, lo cual facilita la subida y bajada de trabajadores.

El problema de utilizar la pendiente de la pirámide es que es muy inclinada (51º 50´); si acometemos con un trineo cargado contra ella simplemente chocaremos. Hay que utilizar rampas intermedias: la primera será de piedra caliza con una inclinación de 15º y, además, se utilizará para anclar la rampa de peldaños; la segunda será de madera con 30 º de inclinación y permitirá la transición a la rampa de peldaños. Podemos verlo en la siguiente figura.

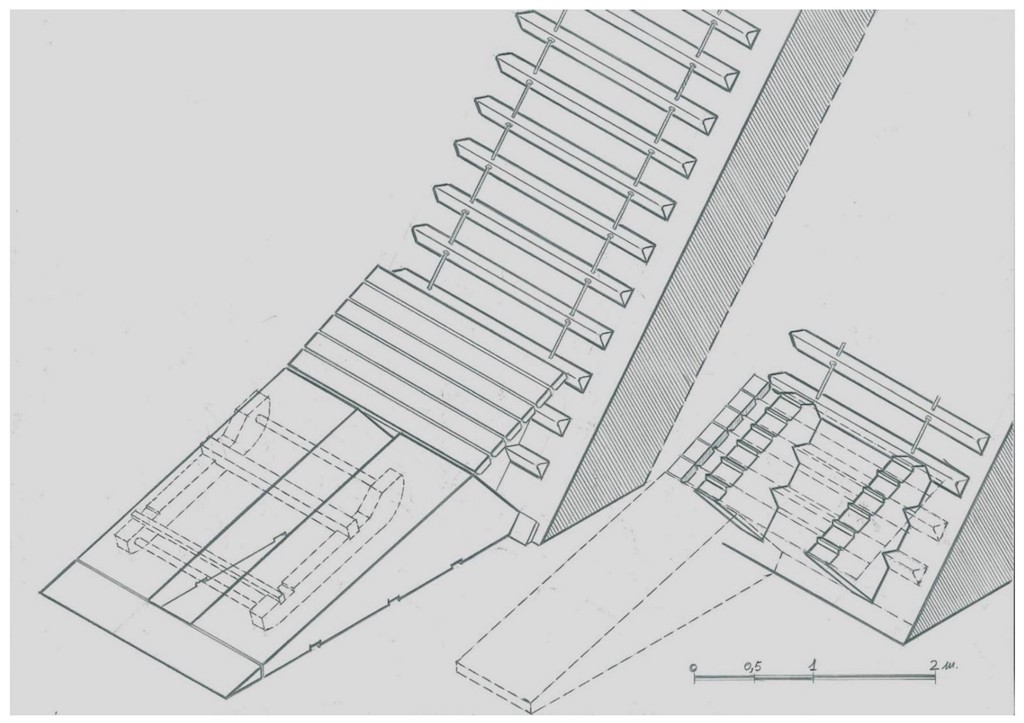Dibujo 12

Para elevar los bloques de piedra caliza se utilizarán trineos de madera que se deslizarán por las rampas inclinadas hasta la hilada correspondiente. Para pasar del plano horizontal al plano inclinado (51º 50´), se dispondrán dos pequeñas rampas adosadas a la base de la pirámide con dos pendientes: de 15º la primera y 30º la segunda. Así conseguiremos una transición controlada del trineo desde el suelo a la cara de la pirámide.

La primera estará compuesta por dos bloques de piedra caliza (según el diseño de la figura) por donde deslizará inicialmente el trineo. Las dos piedras que conforman la rampa se apoyarán contra la cara mediante un tablón de madera que impide el deterioro de la superficie del revestimiento. Esta primera doble rampa estará rematada en su inicio por una cuña longitudinal de madera que atenúa el primer impacto del trineo. En caso de deterioro su reposición sería fácil y económica. Las piedras llevaran unas hendiduras en su base para su colocación, traslado o almacenaje

La siguiente rampa será de madera, está compuesta por dos bloques compactos que descansan sobre las piedras de la primera rampa y sobre la cara de la pirámide. Su función es proteger el revestimiento de caliza blanca y servir de apoyo a la segunda rampa rematada por un entablado de madera con una pendiente de 30º. También sirve para fijar los primeros peldaños de la rampa de madera evitando que el primer impacto desestabilice su colocación.

En el siguiente dibujo se ve el esquema del posicionamiento del trineo sobre la rampa de peldaños.

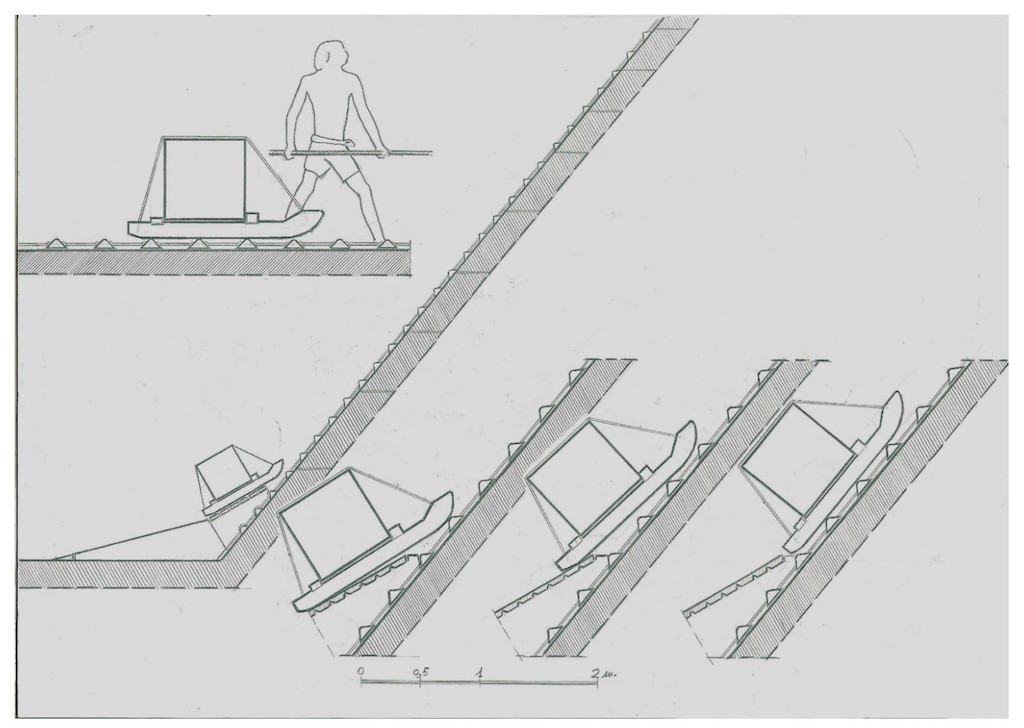 Dibujo 13

En el apartado “1” del dibujo se ve la transición del trineo desde una superficie plana al inicio de la rampa de madera apoyada sobre la cara de la pirámide. Se utilizarán dos pequeñas rampas para pasar de 0º a 51º 50´, que es la pendiente de las caras de la pirámide y donde apoyan las rampas de peldaños. La inclinación de las dos pequeñas rampas será de 15º y de 30º.

En los apartados “2” “3” y ”4” se distingue la posición del trineo con su carga hasta adaptarse a la pendiente de las rampas de peldaños. La curvatura de los patines y el remate en curva de cada uno de los “peldaños” impide un desembarco brusco.

En el apartado “5” se observa la proporción entre el trineo y un trabajador. Hay estudios prácticos en los que con 6 u 8 trabajadores y en superficies horizontales se han movido piedras sobre trineos de hasta 6.000 kg, pero para rampas inclinadas no sería tan sencillo.