Grupo 5: pirámides egipcias con ángulos en torno a los 53º (Seked = 5 ¼)
Con un total de 9 pirámides, este grupo es el que prevalece con diferencia de todos los demás y por ello merece una atención especial. Todo parece indicar que fueron diseñadas sobre la base de los Triángulos Sagrados egipcios, que son aquellos triángulos rectángulos cuyos lados están en la relación 3-4-5, a los que se les atribuían propiedades mágicas o estéticas y de hecho en los nombres de algunas de estas pirámides aparece el trilítero nfr (símbolo F35, según la clasificación de Gardiner), que significa hermoso o bello.
La preferencia por este ángulo de inclinación (poco mas de 53º) la podemos también observar en el papiro matemático de Rhind (RMP). Es el único documento en el que se encuentran problemas referentes a la inclinación de las caras de pirámides. En concreto, los problemas nº 56, 57, 58 y 59, hacen referencia a pirámides de caras lisas en los que se pide calcular el «seked» (inclinación de las caras de la pirámide) a partir de las dimensiones de la pirámide, o viceversa, sabiendo el «seked» y una de sus dimensiones (por ejemplo, el lado), calcular la otra dimensión (altura).
| PROBLEMA | ÁNGULO (*) |
|---|---|
| RMP 56 | 54º 14′ |
| RMP 57 | 53º 8′ |
| RMP 58 | 53º 8′ |
| RMP 59 | 53º 8′ |
(*) NOTA: No se ha incluido en esta tabla el problema nº 60 del papiro matemático Rhind (RMP 60) y el nº 14 del papiro matemático de Moscú (MMP 14), pues los ángulos que se obtienen de ellos son respectivamente 75º 58′ y 80º 34′, propios de pirámides truncadas o escalonadas y no de pirámides de caras lisas como se está considerando.
Donde podemos observar que, en tres de los cuatro problemas conocidos sobre pirámides también utilizaban la pendiente propia del diseño con triángulos sagrados.
Se tiene constancia de que los antiguos egipcios utilizaron este tipo especial de triángulos en muchas de sus construcciones como templos y pirámides, e incluso en dibujos y pinturas. Los mejores ejemplos los tenemos en las 4 pirámides de la VI Dinastía. No obstante, hay muchas otras pirámides, de otras dinastías, en las que también se utilizó, casi todas ellas del Imperio Antiguo, especialmente en la pirámide de Kefrén (IV Dinastía), como primera y mayor pirámide construida en base a estos triángulos.
En concreto las pirámides de este grupo, por orden cronológico de construcción, son:
- Pirámide de JAFRA (Kefrén) en Giza. IV Dinastía.
- Pirámide de USERKAF en Sakkara. V Dinastía.
- Pirámide de NEFERIRKARA-KAKAI en Abusir. V Dinastía.
- Pirámide de DYEDKARA-ISESI en Sakkara. V Dinastía.
- Pirámide de TETI en Sakkara. VI Dinastía.
- Pirámide de MERYRA-PEPY-I en Sakkara. VI Dinastía.
- Pirámide de MERENRA-ANTYEMSAF en Sakkara. VI Dinastía.
- Pirámide de NEFERKARA-PEPY-II en Sakkara. VI Dinastía.
- Pirámide de SEHETEPIBRA-AMENEMHAT-I en el-Lisht. XII Dinastía.
Excepto la ultima, del Imperio Medio, con un ángulo de inclinación de caras de 53º 36′ 56, a todas las demás se les atribuye el ángulo de 53º 7′ 48″ exactamente el de los triángulos 3-4-5 y pertenecen al Imperio Antiguo (III-VI Dinastía).
 Pirámide de Kefren © Johanna Vargas
Pirámide de Kefren © Johanna VargasEn cuanto a tamaños, la de Jafra (Kefrén) en Giza (215,25 m de lado) y la de Neferirkare en Abusir (105 m de lado), son las más grandes, el resto tienen dimensiones muy parecidas (Casi 80 m de lado y unos 52 m de altura), y se localizan en Saqqara, excepto la ultima, la de Amenemhat I, que está en el-Lisht.
Respecto a la geometría de estas pirámides, veremos que el uso de los triángulos 3-4-5 en su construcción reporta importantes ventajas. Una de ellas es que para la resolución de estos triángulos rectángulos, no es necesaria la aplicación del Teorema de Pitágoras, ya que en estos casos, se puede realizar de una manera mucho más sencilla utilizando tan sólo sumas o restas, sin necesidad de elevar números al cuadrado, ni resolver complicadas raíces cuadradas.
Los ángulos interiores de este tipo de triángulos son 90 ? , 36º 52′ 11″ y 53º 07′ 48″. Lo cual quiere decir que cualquier triángulo que posea estos ángulos, independientemente del tamaño que tenga, será un triángulo 3-4-5 o Triángulo Sagrado.
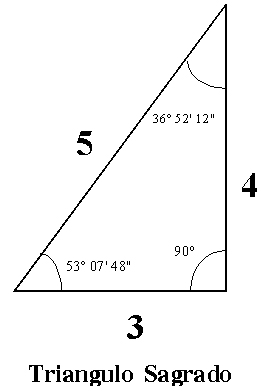
Es fácil demostrar que en este tipo de triángulos se cumplen ciertas relaciones simples. Citaremos algunas, como por ejemplo:
La hipotenusa es igual al cateto menor mas la mitad del cateto mayor.
El cateto mayor es igual al doble de la diferencia de la hipotenusa con el cateto menor.
La hipotenusa es igual a la diferencia que hay entre el doble del cateto mayor con el menor.
Todas estas relaciones son muy fácil de deducir empírica y matemáticamente, pero por otro lado son tan sencillas que es fácil darse cuenta de ellas al poco de manejar y resolver triángulos de este tipo, y que no es improbable que se les ocurriese a los antiguos escribas.
Por otro lado, diseñar un triángulo de este tipo a partir del valor de uno de los catetos, también resulta muy simple, basta multiplicar dicho valor por la fracción ¾, operación bastante sencilla para nuestros escribas, que manejaban con excelente soltura los números fraccionarios. La importancia de esta fracción, es que junto con la de 2/3, son las únicas fracciones de numerador distinto de uno con las que operaban; todas las demás fracciones eran unitarias (de numerador uno), en caso contrario eran reducidas a sumas de fracciones unitarias y por tanto, ambas fracciones, 2/3 y ¾ tenían una consideración especial.
Una de las aplicaciones de los Triángulos Sagrados es que podían utilizarse para construir ángulos rectos, pues la unión de tres palos o barras cuyas longitudes estén en la proporción 3-4-5, forman un triángulo rectángulo. Esto también es posible con la ayuda de una cuerda dividida, con nudos, en doce partes iguales, permitiendo construir un triángulo 3-4-5. En el Museo de El Cairo se encuentran muestras de ello.
Las pirámides diseñadas con Triángulos Sagrados contienen 4 triángulos de este tipo en su estructura, siendo éstos los que se forman con cada uno de los apotemas de las caras, la base y la altura de la pirámide y que precisamente están orientados en la dirección de los 4 puntos cardinales.
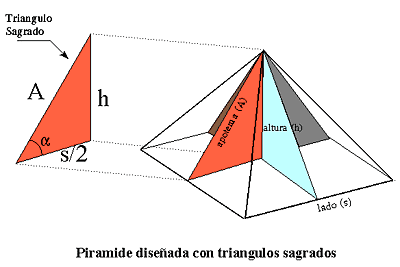
En las pirámides construidas así, es fácil demostrar que la altura que alcanzará es 4/3 del valor de la mitad de su lado, o mejor dicho las 2/3 partes del valor de éste. En efecto, si s es el lado y h la altura, tenemos:
![]()
Despejando h de la ecuación, queda:
![]()
Donde nos aparece la mencionada fracción 2/3. Teniendo esto en cuenta, es fácil predecir cual será la altura final de una pirámide diseñada sobre la base de este tipo de triángulo.
De la misma manera, teniendo en cuenta lo mencionado hasta ahora, en una pirámide de este grupo, es fácil demostrar que:
El apotema es igual a la semisuma del lado y la altura de la pirámide.
![]()
Por tanto, con operaciones muy básicas para nuestros escribas, se simplifican mucho los cálculos para el diseño de pirámides. Por dar un ejemplo, recordemos que el apotema para el resto de las pirámides se calcularía con una expresión mucho más complicada:
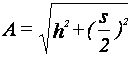
Podríamos decir que los antiguos egipcios han utilizado este tipo de triángulo, no solo por motivos estéticos, como se ha mencionado anteriormente, sino porque facilitaba muchos los cálculos que debían de hacerse en el diseño inicial, en los proyectos previos a las obras. Pero sin embargo, la mayor aplicación práctica de todo esto se encontró en las fases de la construcción. Efectivamente, podemos encontrar dos aplicaciones importantes, fundamentales para que la pirámide adquiera la forma final pretendida:
1) La posición de los bloques de piedra en las hiladas
2) La zona de corte los bloques de revestimiento
La primera de ellas se refiere al calculo del desplazamiento horizontal de los bloques de piedra (no de revestimiento) respecto a los bloques exteriores de la hilada inmediatamente inferior, de tal manera que el cuerpo de la pirámide fuese alcanzando la inclinación de 53º 07′ 48″ propia de los triángulos sagrados. Para ello basta multiplicar la altura del bloque de la hilada superior por la fracción ¾. Puesto que no todos los bloques tenían el mismo tamaño, los cálculos se realizarían en cada una de las hiladas, e incluso se repetirían con bloques de una misma hilada, si éstos tuviesen alturas diferentes.
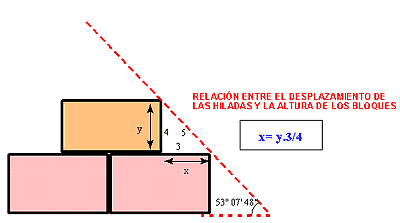
La segunda aplicación se encuentra a la hora de calcular la zona del corte de los bloques de revestimiento de las pirámides. Para darles la inclinación deseada, bastaría con multiplicar el valor de la altura del bloque por la fracción 3/4, tal como se explica en la Figura.
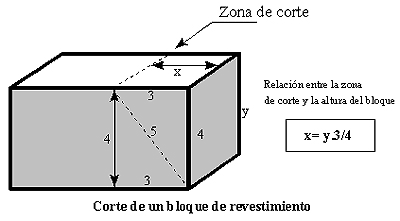
Por ultimo, baste decir que según los procedimientos matemáticos de los egipcios, la multiplicación de un numero por la fracción ¾ o 2/3 eran muy sencillas de realizar. Veamos un par de ejemplos. Multiplicar 28 palmos por ¾. El proceso se basa en duplicar, de tal manera que se parte de la unidad, a la cual le corresponderá en este caso ¾. Se generan, por tanto dos columnas numéricas. Se marcan los valores que suman 28 en la columna de la izquierda, a los cuales les corresponden los marcados en la columna de la derecha. La suma de estos últimos (21) será el resultado buscado:
| 1 | ¾ | |||
| 2 | 1 ½ | |||
| 4 | * | 3 | * | |
| 8 | * | 6 | * | |
| 16 | * | 12 | * | |
| Total: | 28 | 21 | ||
Así por ejemplo si tenemos un bloque pétreo de 28 palmos de altura, bastará desplazarlo 21 palmos, con respecto al bloque de la hilada inmediatamente inferior, para que la inclinación de la pirámide vaya adquiriendo la forma deseada.
Para multiplicar por 2/3, el proceso es similar. Veamos el mismo ejemplo: 28 palmos por 2/3:
| 1 | 2/3 | |||
| 2 | 1 + 1/3 | |||
| 4 | * | 2 + 2/3 | * | |
| 8 | * | 5 + 1/3 | * | |
| 16 | * | 10 + 2/3 | * | |
| Total: | 28 | 18 + 2/3 | ||
El primer paso ha consistido en duplicar 2/3, fracción, de sobra conocida por los antiguos escribas como la suma ½ + 1/6, y por tanto el doble de la misma es 1 + 1/3. El siguiente paso consiste en duplicar esta suma, que lógicamente es 2 + 2/3, y así sucesivamente.
Este mismo tipo de aplicaciones se ha considerado en el grupo de pirámides cuyo seked es 4 ¾, (Grupo 3) es decir cuyo ángulo es poco más de 56º, pues en este caso pueden basarse en un triángulo cuyos catetos están en la relación 2-3 y por tanto, al igual que en el caso anterior, para calcular el desplazamiento horizontal de los bloques basta multiplicar por 2/3 la altura del bloque. Y lo mismo ocurre para determinar el punto de corte de los bloques del revestimiento y darles la inclinación deseada, basta con multiplicar por 2/3 la altura del mismo.
Por ultimo, para finalizar, el uso de los triángulos sagrados bien pudo haber sido como consecuencia de un fenómeno solar: la formación de sombras, pues la necrópolis menfita, donde se elevaron estas pirámides está muy próxima al paralelo 30º del globo terrestre y como consecuencia de ello, cuando el sol del solsticio de invierno, alcanza su máxima altura, se produce la formación de triángulos sagrados de los objetos con su sombra, especialmente los alargados, como obeliscos, o incluso personas de pie y por tanto, es muy probable, que los egipcios, como buenos observadores, conocieran la formación de triángulos sagrados con las sombras en este día tan señalado.



