Grupo 3: pirámides egipcias con ángulos en torno a los 56º (Seked =4 ¾)
Son 4 las pirámides conocidas las que corresponden a este grupo:
La de Unis y la de Jendyer están en Saqqara (V y XIII Dinastías) y las de Senusert III y Amenemhat III en Dashur, ambas de la XII Dinastía.
La pirámide de Unis es la ultima que se construye en la V Dinastía y es la más pequeña del Imperio Antiguo. En ella es donde aparecen por primera vez los llamados «Textos de las Pirámides», pues hasta entonces no se había encontrado ningún texto en el interior de las mismas.
Las pirámides de Senusert III y de su sucesor Amenemhat III, se levantaron en el mismo lugar (Dashur) y coinciden en dimensiones (104 m de lado y 78,5 m de altura). Lo más curioso de ambas es que por primera vez la entrada a la pirámide no se localiza en la cara Norte, si no que la de Senusert III, la tiene en la cara Oeste y la de Amenemhat III tiene dos entradas, una en la cara Sur y otra en la Este.
La pirámide de Jendyer es una de las ultimas y también más pequeñas de las construidas en Egipto y al igual que en las dos pirámides anteriores su entrada no está en la cara Norte, sino que está en la cara Oeste. Es la que tiene el ángulo de caras más pequeño, está más próximo a 55º que a 56º.
Como curiosidad geométrica podemos decir que las caras de estas pirámides son casi triángulos equiláteros, especialmente la ultima, la de Jendyer, pues el ángulo de inclinación de sus caras es algo inferior al de las demás. Todo esto puede observarse comparando los datos de las aristas con los de los lados (pues son muy similares) o bien los ángulos β y δ, (Ver croquis) los cuales son muy próximos a 60º , los que corresponden a los triángulos equiláteros.
Otra particularidad geométrica, más importante que la anterior, se debe precisamente, al ángulo de inclinación de caras (algo mas de 56º, excepto en la pirámide de Jendyer, como se ha mencionado), ya que este ángulo corresponde al de los triángulos rectángulos cuyos catetos están en la proporción 2-3. Exactamente correspondería a un ángulo de 56º 18′.
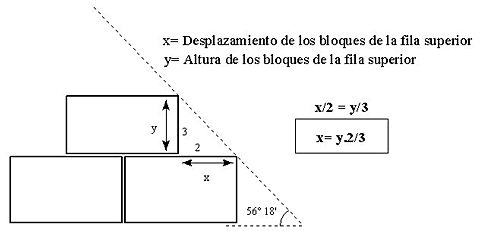
Esto tiene gran importancia en las fases de la construcción, ya que facilita ciertos cálculos. (Lo mismo ocurre con las pirámides del grupo 5, pero en este caso se trata del triángulo sagrado egipcio o triángulo 3-4-5, y cobra más importancia). Así por ejemplo, basta multiplicar la altura del bloque de la hilada superior por la fracción 2/3 para saber el desplazamiento horizontal de los bloques de una determinada hilada, respecto a los bloques exteriores de la hilada inmediatamente inferior, para que de esta manera el cuerpo de la pirámide fuese alcanzando la inclinación de 56º. Ver Figura 1.
Otra de las aplicaciones importantes, se encuentra a la hora de cortar los bloques del revestimiento de las pirámides. Para darles la inclinación deseada, basta con multiplicar el valor de la altura del bloque por la fracción 2/3, tal como se explica en la Figura 2.
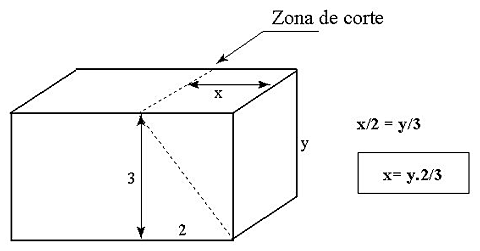
Ni que decir tiene, que dicha multiplicación era perfectamente conocida por los antiguos escribas, amén de la fracción 2/3, que junto con la fracción ¾, eran las únicas fracciones con numerador distinto de la unidad que ellos utilizaban, pues todas las demás fracciones, eran unitarias o suma de ellas.



